LEONARDO PISANO
(FIBONACCI)
Names: Leonardo Pisano (Leonardo of Pisa)
later known as Fibonacci (< filius Bonacci)
Life:
Born: c. 1175 in Pisa
Father: merchant/state official. Leonardo traveled around with his father and learned about and subsequently studied the Hindu "Arabic" number system and mathematics in many of these places.
Died: after 1240
Opera:
Liber Ab(b)aci (autograph manuscript 1202, not extant); revised 1228
(published in Rome in 1857 based on manuscript of 1228 revision)
Practica Geometriae 1220
Liber Quadratorum 1225 (Trans. see below)
Flos 1225
Significance:
Leonardo was one of the most significant figures in the history of mathematics. He is especially known to most people today for the series named after him, the Fibonacci series or sequence. [Take any two numbers. Add these to get the next number. Keep adding the last two numbers to get the next.] The ratio produced by two successive numbers of such a series converges on the Golden Ratio, (approximately .618, indicated by φ, phi, for Phidias), a ratio that is prevalent in nature. His Liber Abbaci, the Book of Calculation, was a manual promulgating the benefits of the Hindu-Arabic number system and teaching its use. It includes proofs for all his methods, as well as numerous practical examples for business use. The most famous example is his problem of how many offspring are produced by a pair of rabbits in one year, which involves a Fibonacci series.
Note regarding the history of number systems:
The ancient Greeks used their alphabet for their number system. The first letter, alpha, was also the symbol (with a mark to indicate that it was to be read as a number rather than the letter) for the number "1;" the second letter, beta, was "2," and so on up to ten, then each successive letter represented a multiple of ten (twenty, thirty, etc.), up to 100; then 200, and so on up to 900. Most of Greek mathematics was done using geometry. Geometry was how Eratosthenes calculated the circumference of the earth. One thinks of the famous Greek mathematicians Euclid, Pythagoras, and Archimedes.
The Babylonians developed a hexadecimal system of numbers. With their easier system, they were able to do their astronomical calculations, which became important for the Greeks and later in the Medieval period. The Greeks, in fact, sometimes used the Babylonian system to calculate, then converted back to the Greek to write down their answer. This Babylonian system also gives us our sixty seconds per minute and sixty minutes per hour.
The Romans also used letters to represent numbers, the well-known "Roman" system of numerals. (I = 1, V = 5, X = 10, L = 50, C = 100, D = 500, and M = 1000). This was the system still being used in the twelfth century.
Another system was that developed in India, but called by us the "Arabic." This is the base ten "decimal" system of 9 digits plus 0 with different values depending on their placement in which column, e.g. 8 ones (=8) or 8 tens (=80). Leonardo Pisano’s father was an Italian merchant (of Pisa, hence the name Pisano). Fibonacci, the name that this mathematician is often known by, is said to be a contraction of "filius Bonacci," ("son of Bonacci"), sometimes traveled with his father or went to port. He learned of this "Indian" system of numbers and realized how much more useful it was for practical calculations. He was not bound by theological doctrine, which was averse to the concept of zero. His Liber Abbaci, or Book of Calculation,(since calculations were often done on an abacus) was a textbook on how to use this system, including word problems. The system quickly caught on with other merchants, despite a ban on its use by officials.
Bibliography
Scritti di Leonardo Pisano, vol. 1. Ed. by Boncompagni. Rome. 1857.
(source Latin text is based on, with my emendations)
Fibonacci’s Liber Abaci. Tr. by Laurence Sigler. New York: Springer. 2002.
Pickler: QA 32. F4713. 2002
Seife, Charles. Zero: The Biography of a Dangerous Idea. Viking, 2000 or New York: Penguin 2000. (Truman Browsing: QA 141. S45. 2000)
The Book of Squares. Tr. by Laurence Sigler. Pickler: QA 32. F4813. 1987
http://plus.maths.org/issue3/fibonacci/ ("The Life and numbers of Fibonacci" by R. Knott, D.A. Quinney and Pass Maths: biography, Fibonacci sequence and ratio)
http://www.malhatlantica.pt/mathis/Europa/Medieval/fibocacci/Liberabaci.htm
(Latin chapter headings)
http://en.wikipedia.org/wiki/Fibonacci (Wikipedia article)
http://faculty.evansville.edu/ck6/bstud/fibo.html (Including the article "Eight Hundred Years Young" by A.F. Horadam from The Australian Mathematics Teacher 31 (1975) 123-134).
Characteristics of Fibonacci’s Latin
Numbers (see below)
3rd conjugation verbs: future (-am, -ēs, etc.)
4th declension nouns: gradus, manus
jussive subjunctive (let _____)
passive verbs (e.g. -tur, -ntur) (is/are ____ed, etc.)
passive infinitives
comparative adverbs (-ius) (inferius, lucidius)
gapping: omitting words in repeated parallel constructions
gerund(ive) (-nd- "_______ing") (decuplando; mutando)
passive periphrastic (gerundive of obligation)
word order: separation of adjectives and nouns
number word with plural verb form
Suffixes: (see Word Formation)
*tiō, -tiōnis, f. (multiplicatiō, descriptiō, demonstratiō, collectio, congregatio)
-tās, tātis, f. (unitās)
-iter (adverb) (leuiter)
-tim (adverb) (gradatim; permutatim)
-ē (adverb) (Arabice)
Orthography/spelling:
u (may) = v
e (may) = ae
-ij = -ii
i/y
xt (may) = xst
Vocabulary:
numbers (see below)
incipit begins
figura digit (vs. numerus, number with absolute value)
quīlibet, quaelibet, quodlibet whatever ____ (pleases you/you want)
and other indefinite pronouns
unitās one’s digit; the digit "1"
gradus place, step, (i.e. column)
uero (postpositive): but (indeed)
ut + indicative or list without verb: as; as (for example)
Gapping:
Primus gradus in descriptione numerorum incipit a destera.
Secundus [ ] uero uersus sinistram sequitur primum.
Tertius [ ] secundum [ ] sequitur.
Quartus [ ] tertium [ ] [ ],
et quintus [ ] quartum [ ] [ ], . . .
si in primo gradu fuerit figura unitatis, unum representat;
si binarii, duo
si ternarij, tria
. . .
usque si nouenarij
. . .
ut si [ ] figura unitatis, centum [ ]
Word order: separated adjectives and nouns (usually by a verb/al or postpositive connector). Adjectives have endings that agree with their noun and they can "bungy" jump over other words:
per suos in infinitum ascendit gradus
in primo reperitur gradu
secundum occupat gradum
hac itaque demonstratione
Roman numerals:
I = 1
V = 5
X = 10 see A&G)
L = 50 (< Greek letter for 50, see A&G)
C = 100
D = 500 (1/2 of old symbol for 1000,
M = 1,000
Smaller numbers to the left of larger numbers are subtracted from the larger. A smaller number may be only one or two characters smaller. e.g.: "I" may be used before V (IV = 4) or X (IX = 9), but not L.
Review of Latin numbers (and preview of terminology and phrasing):
Cardinal:
ūnus, -a, -um: ("pronoun" decl.)
duo (dual declension)
trēs, tria (3rd decl. -i stem pl.)
quattuor
quinque
sex
septem
octō
novem
decem
vigintī = 20 -gint(ā) = _0 (multiple of 10) (note vowel, cf. viginti)
centum = 100 -centī,-ae,-a/-gentī = _00 (multiple of 100) (note vowel: cf. centum)
mīlle = 1,000 (sing. indecl. adj.) mīlia (pl: nt. -i stem noun + gen.)
Ordinal: prīmus, -a, -um, secundus, tertius, etc. (declined adj.; often with -imus or -tus, -a, -um)
-ēnī, -ae, -a: so many units/tens/hundreds, etc. (i.e. ____ column/place)
-(en)-ārius, -a, -um: such and such a (tens/hundreds, etc.) digit, e.g. decenarius = ten’s digit
-iēns: so many times
-plex; -plus: ___-fold
Addition: additatiō, -ōnis, f. or collectiō, -ōnis
addo, -ere (+ cum + ablative)
summa (= "total, sum," because originally written at the summa, top)
Subtraction: extractiō, -ōnis; extrahō, -ere; demō, -ere (+ de + ablative)
residuum (= remainder)
Multiplication: multiplicatiō, -ōnis; multiplico, -are (+ per/ in or contra)
Division: divisio; divido, -ere; divisor; divisus (+ per)
Fibonacci:
zephyrum/zephirum, -i, nt. = 0
figura, -ae: digit (vs. numerus number)
unitās, -tātis: ones’ digit; the digit "one"
Note on text formats:
* in front of a word indicates that it is in the Glossary (see link in top menu))
maroon words have notes; hold the cursor over the word to see the note. Notes with a * indicate that this word occurs again and should be learned; see the Glossary if you don’t remember it the next time.
underlined blue are links (from a link at the bottom of a page, click on the line number or word to get back to the place in the text that the linked note is for)
FIBONACCI
LIBER AB[B]ACI
Explicit prologus. Incipiunt capitula.
De cognitione nouem figurarum Yndorum, et qualiter cum eis omnis numerus scribatur;
et qui numeri et qualiter retineri debeant in manibus, et de introductionibus abaci.
De multiplicatione integrorum numerorum.
De additione ipsorum ad inuicem.
De extractione minorum numerorum ex maioribus.
De divisione integrarum (sic) numerorum per integros.
De multiplicatione integrarum (sic) numerorum cum ruptis atque ruptorum sine sanis.
De additione ac extractione et diuisione numerorum integrarum cum ruptis atque partium numerorum in singulis partibus reductione.
De emptione et venditione rerum uenalium et similium.
De baractis rerum uenalium et de emptione bolsonalie, et quibusdam regulis similibus.
De societatibus factis inter consocios.
De consolamine monetarum atque eorum regulis, que ad consolamen pertinet.
De solutionibus multarum positarum questionum quas erraticas appellamus.
De regula elcataym qualiter per ipsam fere omnes erratice questiones soluantur.
De reperiendis radicibus quadratis et cubitis ex multiplicatione et diuisione seu extractione earum in se, et de tractatu binomiorum et recisorum et eorum radicum.
De regulis proportionibus geometrie pertinentibus: de questionibus aliebre et almuchabale.
Incipit primum capitulum.
Nouem figure Indorum he sunt
9 8 7 6 5 4 3 2 1
Cum his itaque nouem figuris, et cum hoc signo 0, quod Arabice "zephirum " appellatur, scribitur quilibet numerus, ut inferius demonstratur. Nam numerus est unitatum perfusa collectio siue congregatio unitatum, que per suos in infinitum ascendit gradus. Ex quibus primus ex unitatibus, que sunt ab uno usque in decem, constat. Secundus ex decenis, que sunt a decem usque in centum, fit. Tertius fit ex centenis, que sunt a centum usque in mille. Quartus fit ex millenis que sunt a mille usque in decem milia, et sic sequentium graduum in infinitum, quilibet ex decuplo sui antecedentis constat. Primus gradus in descriptione numerorum incipit a destera. Secundus uero uersus sinistram sequitur primum. Tertius secundum sequitur. Quartus tertium, et quintus quartum, et semper sic uersus sinistram gradus gradum sequitur. Figura itaque que in primo reperitur gradu se ipsam representat, hoc est: si in primo gradu fuerit figura unitatis, unum representat; si binarii, duo; si ternarij, tria, et ita per ordinem que secuntur, usque si nouenarij: nouem figure quidem que in secundo gradu fuerint, tot decenas representant, quot in primo unitates; hoc est si figura unitatis secundum occupat gradum, denotat decem; si binarij, uiginti; si ternarij, triginta; si nouenarij, nonaginta.
Figura namque que in tertio fuerit gradu, tot centenas denotat, quot in secundo decenas, uel in primo unitates, ut si figura unitatis centum; si binarij, ducenta; si ternarij, trecenta, et nouenarij nongenta.Ipsa igitur que fuerit in quarto gradu tot millenas quot in tertio centenas, aut in secundo decenas, uel in primo unitates denotat; et sic semper mutando gradum, numerus decuplando ascendit. Et ut hoc quod dictum est lucidius declarescat, ipsum cum figuris ostendatur.
Si figura septenarij fuerit in primo gradu, et ternarij in secundo, ambe insimul 37 denotant; uel econtra: figura ternarij in primo, et septenarij in secundo, 73 denotabunt. Item si figura quaternarij fuerit in primo, et unitatis in secundo sic 14, nimirum .XIIII. denotabunt: uel si figura unitatis fuerit in primo, et quaternarij in secundo sic 41, denotabunt XLI. Rursus in primo [septenarii] et [binarii] in secundo faciunt 27; contrarium enim facit 72. Si autem septuaginta tantum scribere uoluerit, ponat in primo gradu 0, et post ipsum ponat figuram septenarii, sic 70; si octuaginta, sequatur zephyrum figuram octonarij sic 80: hac itaque demonstratione quemlibet numerum a decem usque in centum cum duabus figuris scribere potes.
Cum tribus uero a centum scribatur usque in mille ; ut si figura octonarii fuerit in primo, et quinarii in secundo, et unitatis in tertio, 158, centum quinquaginta octo denotabunt; et econuerso: si figura unitatis fuerit in primo, et quinarii in secundo, et octonarii in tertio 851, octigenta et quinquaginta unum denotabunt; uel econtra : si figura octonarii fuerit in primo, et unitatis in secundo, et quinarii in tertio, denotabunt 518. Item si permutatim figura quinarii fuerit in primo, octonarii in secundo, et unitatis in tertio, denotabunt 185. Item si figura unitatis fuerit in primo, octonarii in secundo, et quinarii in tertio, nimirum denotabunt 581: tres uero unitates sic 111, centum undecim faciunt.
Verum si quinquagenta tantum scribere uolueris, in primo et in secundo gradu ponas zephyra, et in tertio figuram quinarii hoc modo 500; et sic cum duobus zephyris quemlibet centenariorum numerum scribere poteris. Et si centenaria cum decenis sine unitatibus scribere uolueris, ponas in primo gradu zephyrum, in secundo decenas, et in tertio centenas quas uolueris. Verbi gratia: si in primo gradu fiat zephyrum, et in secundo figura nouenarii, et in tertio binarii, denotabunt 290. Si autem absque decenis centenaria cum unitatibus scribere uolueris, pones in secundo gradu, scilicet in loco decenarii zephyrum, et in primo numerum unitatum quem uoluerit, et in tertio centenariorum: ut si in primo fuerit figura nouenarii, et in secundo zephyrum, et in tertio binarii 209; et sic secundum supradictum demonstrationem qualem uolueris numerum a centum usque in mille scribes cum tribus figuris. Cum quattuor *namque a mille usque in decem milia, ut in sequenti cum figuris numeris super notatis ostenditur.
![]()
Et sic in reliquis numeris est procedendum. Cum quinque namque figuris scribuntur omnes numeri, incipiendo a decem milia usque ad centum milia. Cum sex uero, a centum milibus usque in mille milia, et sic deinceps, addendo figuram figuris, numerus gradatim in decuplum ascendit. Vnde si *contigerit quod aliquem numerum multarum figurarum propter multitudinem figurarum, quis legere uel intelligere nequeat, qualiter legere et intelligere ipsum debeat, ostendere procurabo.
. . . (folio 4 verso)
Prescriptas itaque in tabulis iunctiones et multiplicationes in manibus addiscendo semper utantur colligere, vt animus pariter cum manibus in additationibus et multiplicationibus quorumlibet numerorum expeditior fiat.
Incipit capitulum secundum de multiplicatione integrorum numerorum.
Capitulum secundum de multiplicationibus integrorum numerorum in octo partes diuidimus, ut differentie atque proprietates earum melius intelligantur. Quarum prima pars erit de multiplicatione duarum figurarum contra duas, atque unius figure contra plures. Secunda de multiplicatione trium figurarum contra tres, atque duarum figurarum in tribus. Tertia de multiplicatione quattuor figurarum contra quattuor, etiam et duarum figurarum et trium in quattuor figuris. Quarta de multiplicacione quinque figurarum in quinque. Quinta de multiplcatione plurium figurarum quam quinque, qualiter multiplicentur ad inuicem. Sexta de multiplicatione numerorum secundi gradus per numeros eiusdem gradus, hoc est duarum figurarum per duas, atque unius figure contra plures, qualiter cordetenus in manibus multiplicentur. Septima de multiplicatione trium figurarum per tres similiter *qualiter in manibus cordetenus multiplicentur. Octaua de multiplicatione omnium numerorum alium modum.
Incipit pars prima de multiplicatione duarum figurarum contra duas.
Numerus se ipsum multiplicare dicitur, quando similis per similem multiplicatur, ut 12 per 12, uel 26 per 26. Numerus numerum multiplicare dicitur, quando numeri se inuicem multiplicantes fuerint ad inuicem inequales, ut 12 per 37 et 46 per 59: denique nos primum numeros secundi gradus ut promisimus, *scilicet a 10 usque in centum in semetipsos multiplicare doceamus. Cum autem uis multiplicare aliquem numerum secundi gradus per aliquem numerum eiusdem gradus, siue equales sint numeri, siue inequales, scribes numerum sub numero, ita ut similis gradus sit sub simili gradu; et si numeri sunt inequales, sit maior sub minore, et incipiat multiplicationem a primo gradu numerorum in tabula prescriptorum. Siquidem multiplicet figuram primi gradus superioris numeri in tabula prescripti per figuram primi gradus subterioris, et scribantur unitates super primum gradum numerorum prescriptorum, et per unam quamque decenam retineat in manu sinistra unum: deinde multiplicet figuram primi gradus superioris numeri per figuram secundi gradus, per ultimam scilicet subterioris numeri, et econtra: figura primi gradus subterioris multiplicetur per ultimam figuram superioris, et addantur in manu cum seruatis decenis; et iterum unitates scribantur super secundum gradum, et retineatur in manu decene. Item multiplicetur ultima figura superioris numeri per ultimam subterioris, et quod ex multiplicatione euenerit cum seruatis decenis in manu super addatur, et unitates in tertio gradu et decene super fuerint in quarto ponantur, et habebitur multiplicatio quorumlibet numerorum a decem usque in centum.
| Verbi gratia: ut si quesierit multiplicationem de 12 in 12, scribantur 12 bis in tabula dealbata in qua littere leuiter deleantur, sicuti in hac margine scriptum cernitur, primus gradus subterioris numeri sub primo superioris, hoc est figura binarii sub figura binarii, et secundus gradus subterioris sub secundo superioris, *scilicet figura unitatis sub figura unitatis, et multiplicet binarium per binarium, erunt 4, que ponat super utrumque binarium ut in prima descriptione posita sunt. Iterum multiplicentur superiora [per 1] qui est in secundo gradu inferioris numeri, erunt 2 que seruentur in manu, et multiplicet iterum 2 subterioris numeri per 1 superioris, erunt 2; que addat cum duobus superius seruatis, erunt 4, que ponat super unitatem utramque; facient ipsa 4 secundum gradum, post priora posita 4 que fecerant primum gradum, ut in secunda descriptione describitur; et adhuc multiplicetur 1 de superiori numero per unum de subteriori, faciet 1; quod 1 scribatur in tertio gradu, scilicet post 44 descripta, ut in tertia et ultima descriptione ostenditur. Et in tot ascendit multiplicatio de 12 in se ipsa, scilicet 144. |
|
Iterum ut lucidius clarescat, 37 per 37 multiplicentur. Scribantur quidem 37 sub 37, ut superius de 12 diximus, et multiplicentur 7 per 7, erunt 49: ponatur itaque 9 super utrumque 7 ut in prima descriptione ostenditur, et pro quattuor de decenis, que sunt in 49, seruentur 4 in manu, et multiplicentur 7 de superiori numero per 3 de inferiori, et 7 de inferiori per 3 de superiori et iungantur insimul, erunt 42, quibus additis cum 4 superius seruatis, erunt 46: scribantur unitates de 46, que sunt 6 super utrumque 3, ut in secunda descriptione denotatur. Et 4 pro quattuor decenis que sunt in 46 in manu seruentur, et adhuc multiplicentur 3 de superiori numero per 3 de inferiori erunt 9; que adde cum 4 modo in manu seruatis, erunt 13: ponantur 3 de 13 in tertio gradu et 1 in quarto, ut continetur in tertia et ultima descriptione. |
|
[Method of checking by casting out nines]
Que multiplicatio, si recta est, ita cognoscitur. Iungantur quidem figure que sunt in superioribus 37, *scilicet 3 cum 7, erunt 10, de quibus dematur 9, remanebit 1, quod seruetur. Eodemque modo colliganturfigure de 37 inferioribus, et demantur inde 9, remanebit similiter 1: multiplicetur ergo 1 quod remansit de superioribus 37 per 1 quod remansit de inferioribus, faciet 1, quod uocetur pensa uel portio, et seruetur in tabula super ipsam multiplicationem, ut in tertia descriptione cernitur: postea colligantur figure que sunt in summa multiplicationis, et de collecta quantitate demantur 9 quotiens potuerit; et si 1 remanebit sicuti pro pensa seruatum est, recta utique erit multiplicatio.
Verbi gratia: ut si iunximus figuras que sunt in summa multiplicationis, scilicet 1 et 3 et 6 et 9, erunt 19, de quibus extrahe bis nouenarium, remanebit 1, ut pro pensa prediximus eum debere remanere: uel de dictis 19 dele 9 que sunt in primo gradu ipsorum, remanebit similiter 1. Et nota cum additis figuris de 37, scilicet 3 cum 7, tunc diuidis 37 per 9, de qua diuisione remanet 1, sicut remansit ex 10 que procreata fuerint ex additione 3 et 7, cum ex eis extracta fuerunt 9: nam residuum quod remanet ex quouisnumero diuiso per 9, est summa que ponitur ex additatione omnium figurarum facientium ipsum numerum.
Et notandum rursus, cum aliquis numerus dividitur in partes, et una queque partium multiplicatur per aliquem numerum, sunt ille multiplicationes in unum collecte equales multiplicationi totius numeri divisi in numerum, in quem multiplicate fuerunt omnes partes ipsius. Ergo multiplicationes de 36 per 37, et de 1 per 37 in unum coniuncte, equantur multiplicationi de 37 in 37. Sed ex multiplicatione de 37 in 37 provenit numerus qui creatus est ex aliqua multitudine nouenariorum, cum 36 sint concreta ex nouenariis. Quare numerus surgens ex 36 in 37, si divisus fuerit per 9, nichil ex eo remanebit indivisibile.
Item multiplicatio de 1 in 37, est equalis summe multiplicationis de 1 in 36 et de 1 in 1. Sed ex multiplicatione de 1 in 36 provenit numerus qui integraliter dividitur per 9: multiplicatio ergo de 1 in 1, scilicet 1, remanet indivisibilis per 9. Ergo de 37 in 37 divisa per 9 remanet 1, quod habetur ex collectione figurarum omnium que sunt in summa de 37 in 37, ut superius invenimus.
…
Incipit capitulum tertium de additione integrorum numerorum.
Cum autem *quoslibet numeros et quotcumque quis addere uoluerit, collocet eos in tabula, secundum quod in multiplicationibus numerorum prediximus, hoc est primum gradum cunctorum numerorum quos addere uoluerit sub primo ipsius qui ante in iunctionem positus fuerit. Et secundum sub secundo, et deinceps quisecuntur. Et tunc incipiat in manibus colligere numeros figurarum que in primis gradibus cunctorum numerorum que in iunctionem positi fuerint, ab inferiori numero usque ad su|periorem, ascendendo: ponat itaque unitates super primum gradum numerorum et decenas in manu reseruet, quibus decenis superaddat numeros qui in secundis gradibus extiterint, et ponat unitates super secundum gradum, et iterum decenas reseruet. Cum quibus collectionem tertii gradus numerorum super addat, et sic ponendo unitates, et decenas reseruando, gradatim numeros colligendo, potest collectionem cunctorum numerorum usque ad infinitum habere. Et ut melius intelligatur iunctiones duorum numerorum et etiam tertij, nec non et plurium ostendantur. . . .
| Ut si quesieris scire ad[d]itationem de 25 cum 49 collocet 49 sub tamque deberet eos ad inuicem multiplicare, et addat 9 cum 5, erunt 14: ponat 4 super primum gradum et pro decenis reservet in manu 1 quod addat cum 4 et cum 2, erunt 7 que ponat, et sic habebuntur pro eorum collectionem 74, ut hic ostenditur.
Item si uoluerit scire collectionem de 123 cum 4567, describat eos ut hic cernuntur; et addat 7 cum 3, erunt 10; ponat 0 et retineat 1 quod addat cum 6 et cum 2, erunt 9, que ponat. Item addat 5 cum 1 que sunt in tertio qradu, erunt 6 que ponat super eundem gradum, et per 4 que sunt in quarto gradu inferioris numeri, ponet 4 in quarto gradu exeuntissumme, cum non sit aliqua figura super ipsa in alio numero, scilicet in 123 et sic habebit pro eorum additatione 4690… |
|
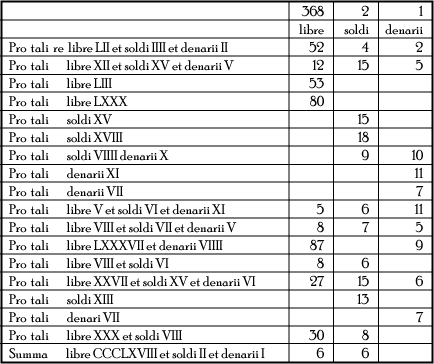
[Method of bookkeeping]
Cvm autem, secundum prescriptam iunctionis doctrinam, numeros adhibet quis sciverit, et uoluerit colligere summas expensarum nauium et similium in quibus continentur libre et solidi et denarii. Intelligat acamerario uel scriba, uel a renuntiatore, *secundum quod dicitur singulariter expensas, uel emptiones singulariter quarumlibet rerum; et describat in tabula linealiter pretium unius cuiusque rei collocans libras sub libris, soldos sub soldis, denarios sub denariis expensarum unius cuiusque faciei, uel cautele; et tunc faciat se optime ab ipso qui expensas renuntiat abscultari, ne forte aliquam fallaciam scripserit in tabula; et correcta in tabula descriptione expensarum colligat omnes denarios, et faciat inde soldos; et quartis [denarios] qui superfuerint [factis] soldis reseruet et factis soldis, describat sub soldis in tabula et colligat eos, et de eorum summa faciat libras, quas ponat inferius in lineatione librarum: et soldis qui superfuerint factis libris super soldos post denarios seruatos reseruet: post hec accipiat summam librarum; et sic habebit summam ipsius pagine uel cartule.
Verbi gratia: ut si quidam renuntiet in quadam expensa quod dedisset in tali et in talibus rebus, ut in sequenti pagina denotatur, adiscat scribere numeros librarum, soldorum et denariorum, sicut in eadem pagina describuntur, in qua pagina denarii qui sunt in ea sunt in summa 73, qui sunt soldi 6 et denarii 1: cum quibus soldi[s] 6 juncti soldi, qui sunt in eadam pagina, fiunt 122, qui sunt libre 6 et soldi 2; et cum ipsis libris 6 colligat libras, reperiet in summa libras 368: est ergo summa librarum omnium soldorum et denariorum insimul iunctorum libre 368 et soldi 2 et denarii 1 que summa est reseruanda in fine pagine, de qua e[x]pensa collecta est; et sic per ordinem colligat expensas per paginas et unicuique pagine summam faciendo: post hec rescribat in tabula summas cunctarum paginarum, et faciet inde summam summarum; et sic poterit colligere quaslibet expensas bizantiorum, et karatorum, et auri unciarum, et tarenorum genouinorum, cantariorum, etiam et rotulorum et cunctarum rerum numeris adiacentium.
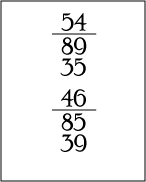
Incipit capitulum quartum de extractione minorum numerorum de maioribus.
Cum autem numerum de numero quis extrahere uoluerit, describat minorem numerum sub maiori, collocans similes gradus sub similibus, et incipiat extrahere primam figuram minoris numeri de prima maioris; et ponat super habundantem numerum super primas figuras. Et secundam extrahat de secunda, et ponat residuum super secunda, et tertiam de tertia. Et reliquas de reliquis per ordinem, semper residua ponendo. Et cum figura minoris numeri, de figura eiusdem gradus maioris numeri extrahi non ualuerit, ideo quia ipsa de minori numero maior erit in eodem gradu quam ipsa de maiori: tunc figure maioris numeri addendus est decenarius, et de coniuncto numero, figura minoris numeri erit extrahenda. Et pro iunctione dictidecenarii in manu unitas erit reseruanda. Et ipsa sequenti figure minoris numeri super addenda etconcreata quantitas de superiori figura eiusdem gradus, si possibile fuerit, erit extrahenda: sin autem de addito decenario, ut supradiximus, extrahatur; et sic gradatim usque ad ultimam figuram minoris numerioperando erit gradiendum: et si maior numerus minorem in gradibus super habundauerit, figure que in ipsis gradibus extiterint, in fine erit ponendus. Et sic habebitur residuum de quorumlibet extractionibus numerorum.
| Verbi gratia, ut si uoluerit quis de 89 extrahere 35, ponantur 35 sub 89, ut in hac margine ostenditur: extrahantur itaque 5 de 9, remanent 4, quem (sic) ponatur super 9, et extrahantur 3 de 8, remanent 5 que ponat super et sic habebuntur per residuoposite extractionis 54: et si 39 de 85 extrahere uoluerit, descriptis numeris, extrahat 9 de 5, quod est impossibile. Vnde addat 10 eiusdem 5, erunt 15, de quibus extrahat 9, remanent 6 que ponat; et pro additis 10, retineat in manu 1 quod addat cum 3, erunt 4 que extrahat de 8, remanent 4, quem ponat super dictam 8, et sic habebit 46 pro residuo posite extractionis. … |
|
. . . . . . . . . . . . . . . . . . . . .
Caput duodecimum (de questionibus abbaci)
. . . . . . . . . . . . . . . . . . . . .
Incipit capitulum octauum de reperiendis preciis mercium per maiorem guisam.
In omnibus itaque negotiationibus quattuor numeri proportionales semper reperiuntur, ex quibus tres sunt noti, reliquus uero est ignotus: primus quidem illorum trium notorum numerorum est numerus uenditionis cuiuslibet mercis, siue constet numero, siue pondere, siue mensura. Numero quidem ut centum coria, uel centum beccune et similium: pondera quoque ut cantarum, uel centum, uel libre, aut unce et similium. Mensura quidem ut metra olei, sextaria frumenti, et canne panni et similium. Secundum autem est pretium illius uenditionis, hoc est illius primi numeri, siue sit quantitas quorumlibet denariorum, siue bizantiorum, siue tarenorum, uel alicuius alie currentis monete. Tertius uero quandoque erit aliqua eiusdem uendite mercis quantitas, cuius pretium, scilicet quartus numerus, ignoratur; et quandoque erit aliqua similis quantitas secundi pretii, cuius merces, scilicet quartus ignotus numerus, iterum ignorabitur. Quare, ut ignotus numerus per notos reperiatur, talem in omnibus tradimus regulam uniuersalem, uidelicet ut in capite tabule, in dextera parte scribas primum numerum, scilicet mercem; retro in eadem linea ponas pretium ipsius mercis, uidelicet secundum numerum; tertium quoque si fuerit mercis, scribe eum sub merce, scilicet sub primo; et si fuerit pretium, scribe eum sub pretio, uidelicet sub secundo; ita tamen, ut sicut fuit ex genere ipsius, sub quo scribendum est, ita etiam sit ex qualitate uel ex quantitate ipsius in numero, uel in pondere, uel in mensura; hoc est si superior numerus, sub quo scribendus est, fuerit numerus ipsorum, et ipse similiter fiat rotulorum; si librarum, librarum; si uncearum, uncearum; si cannarum, cannarum. Et si fuerit numerus soldorum, et ipse sit numerus soldorum; si denariorum, denariorum; si tarenorum, tarenorum; et si bizantiorum, bizantiorum. Quibus ita descriptis, euidentissime apparebit, quod duo illorum positi erunt semper ex aduerso, que insimul multiplicentur; et summa multiplicationis eorum, si per reliquum tertium numerum diuidatur, quartus ignotos nimirum inuenietur: et ut hoc apertius intelligatur, cum diuersis mercibus et pretiis, in sequentibus explanabimus.
Sed primum ostendam, vnde hic modus procedit: sunt enim, ut dixi, in negotiationibus IIIIor numeri proportionales, scilicet, ut sicut primus est ad secundum, ita tertius ad quartum, hoc est, sicut numerus alicuius quantitatis mercis est ad numerum quantitatis sui pretii, ita numerus cuiusuis quantitatis eiusdem mercis ad numerum sui pretii: uel sicut aliqua quantitas cuiusuis mercis est ad quamuis quantitatem eiusdem mercis, ea est pretii unius ad pretii alterius: et cum ita IIIIor quantitates proportionales sunt, erit multiplicatio secunde in tertiam equa multiplicacioni prime in quartam, ut in arismetricis, et geometria probatum est: quare si quarta quantitas est ignota tantum, ex multiplicatione quidem secunde quantitatis in tertia diuisa per primam, nimirum ex diuisione, quarta quantitas prouenit: quare cum diuiditur aliquis numerus per aliquem numerum, et ex diuisione aliquid proueniat; si proueniens in diuisorem | multiplicaueris, nimirum diuisus numerus inde proueniet. Similiter si tertia quantitas ignoratur, diuidenda est per tertiam multiplicatio prime in quartam: et ut ea, que ad negotiationes pertinent, perfecte in hoc libro habeantur, hoc capitulum in quattuor partes diuidimus; quarum prima erit in uenditione cantarium, et earum rerum, que ad pondus uel numerum uenduntur; secunda in eis que ad toloneum seu ad cambium pertinent, ut soldus, libra, uel marca argenti, uncia auri et similia; tertia in uenditione cannarum, ballarum, torscelli et similium; quarta pars erit in reductione Rotulorum unius cantaris ad Rotulos cuiuslibet alterius cantarium, secundum eius diuersitatem.
…
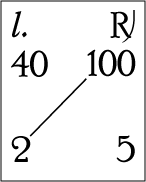
De eodem cum queritur merces de libris.
| Item Rotuli 100 per *libras 40; quot Rotulos habuero per libras 2: quia in his tribus numeris duo sunt ex genere pretii, scilicet libre 40, et libre 2, et alter est ex genere mercis, describantur 40 et 100 in una linea; ideo quia dicitur Rotuli 100 per libras 40: deinde libre 2 describantur sub libris 40, ut erunt numeri eiusdem generis, unus sub alio, ut in hac secunda descriptione cernitur: et multiplica numeros qui sunt ex aduerso, scilicet 100 per 2, erunt 200; que diuide per 40, exibunt Rotuli 5 pro merce illarum 2 librarum, quos describe sub Rotulis 100. |
|
Quot paria coniculorum in uno anno ex uno pario germinentur.
| Qvidam posuit unum par cuniculorum in quodam loco, qui erat undique pariete circundatus, ut sciret, quot ex eo paria germinarentur in uno anno: cum natura eorum sit per singulum mensem aliud par germinare; et in secundo mense ab eorum natiuitate germinant. Quia suprascriptum par in primo mense germinat, duplicabis ipsum, erunt paria duo in uno mense. Ex quibus unum, silicet primum, in secundo mense | geminat; et sic sunt in secundo mense paria 3; ex quibus in uno mense duo pregnantur; et geminantur in tercio mense paria 2 coniculorum; et sic sunt paria 5 in ipso mense; ex quibus in ipso pregnantur paria 3; et sunt in quarto mense paria 8; ex quibus paria 5 geminant alia paria 5: quibus additis cum pariis 8, faciunt paria 13 in quinto mense; ex quibus paria 5, que geminata fuerunt in ipso mense, non concipiunt in ipso mense, sed alia 8 paria pregnantur; et sic sunt in sexto mense paria 21; cum quibus additis parijs 13, que geminantur in septimo, erunt in ipso paria 34, cum quibus additis parijs 21, que geminantur in octauo mense, erunt in ipso paria 55; cum quibus additis parijs 34, que geminantur in nono mense, erunt in ipso paria 89; cum quibus additis rursum parijs 55, que geminantur in decimo, erunt in ipso paria 144; cum quibus additis rursum parijs 89, que geminantur in undecimo mense, erunt in ipso paria 233. Cum quibus etiam additis parijs 144, que geminantur in ultimo mense, erunt paria 377, et tot paria peperit suprascriptum par in pr[a]efato loco in capite unius anni. Potes enim uidere in hac margine, *qualiter hoc operati fuimus, scilicet quod iunximus primum numerum cum secundo, uidelicet 1 cum 2; et secundum cum tercio; et tercium cum quarto; et quartum cum quinto, et sic deinceps, donec iunximus decimum cum undecimo, uidelicet 144 cum 233; et habuimus suprascriptorum cuniculorum summam, uidelicet 377; et sic posses facere per ordinem de infinitis numeris mensibus. |  |
Notes:
Capitulum secundum, pars prima
retineat in manu sinistra: "Let one retain in the left hand" (by using finger counting positions). This was a physical system of carrying. The use of finger positions for counting and calculating was common. Bede (c. A.D. 673-735) describes the system in his De temporum ratione (capitulum I: See link to text with diagram similar to that in one of the manuscripts of Fibonacci’s Liber Abaci). Nicolas Artavasdas (also known as Rhabdas)of Smyrna, 14th century A.D., describes a similar system in his work (Loeb, Greek Mathematical Works, vol. I, pp. 30-35). The left hand was used for smaller numbers; the same positions in the right hand indicated larger numbers.
Capitulum duodecimum: de quaestionibus abbaci
qualiter This kind of sequence of numbers (formed by adding the last two each time to get the next number) is called a "Fibonacci" sequence. The ratio between each succeeding pair of numbers approaches the Golden Ratio of .618. See the links at the end of the Bibliography above.